Pengerian KPK dan FPB

Pada artikel kali ini kita akan membahas mengenai materi KPK dan FPB yang dahulu pernah dipelajari di kelas SD. Materi FPB dan KPK ini sangatlah berguna meskipun terlihat simpel dan mudah tapi banyak sekali kegunaannya. Tetapi sebelum kalian memahami mengenai KPK dan FPB alangkah baiknya kalian terlebih dahulu memahami mengenai Kelipatan, Faktorisasi Prima, dan Faktor Kelipatan.

    1.      Pengertian KPK

KPK merupakan singkatan dari Kelipatan Persekutuan terKecil. jika dilihat dari singkatannya KPK ini mencari bilangan kelipatan persekutuan terkecil dari dua bilangan. Atau bisa kita simpulkan juga bahwa Ketika kita mencari KPK dari 2 buah bilangan maka kita akan mencari nilai kelipatan dari dua bilangan tersebut yang paling terkecil. Dalam mencari nilai KPK ini ada 2 cara, yaitu

1)      Cara Manual

Dengan cara ini kita akan mencari KPK dari 2 buah bilangan dengan cara manual yaitu dengan cara mengkalikan setiap bilangan sampai terdapat kelipatan yang sama.

Contoh KPK dari 2 dan 7

 

Terlihat bahwa kelipatan terkecil dari 2 dan tujuh yaitu 14. Jadi KPK dari 2 dan 7 mengunakan cara manual di dapat 14.

2)      Faktorisasi Prima

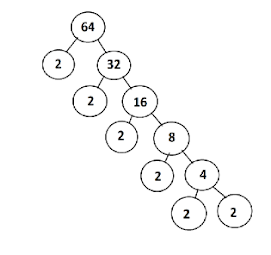
Selain mencari nilai KPK dengan cara manual seperti di atas ada juga cara untuk mempermudah kita dalam mencari nilai KPK dari 2 bilangan atau lebih. Cara yang akan digunakan yaitu dengan memanfaatkan pohon faktor untuk melakukan Faktorisasi Prima.

Ø  Contoh KPK dari 2 dan 7

Langkah Pertama yaitu kita ubah 2 dan 7 kedalam bentuk perkalian dengan faktorisasi prima yaitu mengubah bilangan menjadi kedalam bentuk perkalian. Kita bisa memanfaatkan pohon faktor untuk mempermudah. Tapi disini karena 2 dan 7 merupakan bilangan prima maka faktorisasi prima nya yaitu bilangan itu sendiri. Maka untuk mencari kpk dari 2 dan 7 kita hanya perlu mengkalikan nya saja. Jadi KPK dari 2 dan 7 yaitu 2 x 7 = 14. 

Ø  Contoh KPK dari 8 dan 12

Langkah awal kit acari Faktoriasis Prima dengan cara pohon faktor.

Setelah menyelsaikan pohon faktor kita dapat menuliskan

8   = 2 x 2 x 2  atau 2³

12 = 2 x 2 x 3  atau 2² x 3

Untuk mencari KPK kita ambil semua faktor dan jika ada yang sama kita ambil yang terbesar yaitu 2³ x 3 = 24. Jadi KPK dari 8 dan 12 yaitu 24. Dengan metode ini kitab isa mempersingkat waktu dari pada kita mengerjakan dengan manual seperti cara pertama. Dan cara ini sangat efektif Ketika kita mencari nilai KPK yang besar. 

    2.      Pengertian FPB

       Setelah kita tau mengenai KPK sekarang kita akan mempelajari materi yang sangat penting juga yaitu FPB. FPB atau Faktor Persekutuan terBesar merupakan bilanga bulat           positif terbesar yang dapat membagi habis 2 bilangan atau lebih. Atau dengan istilah lain nilai dari FPB ini yaitu bilangan terbesar yang dapat membagi habis bilangan tertentu. Dalam mencari FPB ada 2 cara yang akan kita gunakan kali ini, yaitu

1)      Cara Manual

Dengan car aini kita dapat mencari nilai FPB secara manual. Sebagai contoh yaitu kita akan cari FPB dari 24 dan 32.

Ø  Pertama kita cari angka yang dapat membagi 24 dan 32 dari yang terkecil.

24 = 2, 4, 6, 8, 12, 24

32 = 2, 4, 8, 16, 32       

Telihat dari pembagian 2 bilangan di atas angka 8 merupakan bilangan terbesar yang dapat membagi 24 dan 32. Maka FPB dari 24 dan 32 yaitu 8.

2)      Cara Faktorisasi Prima

Untuk mencari nilai FPB kita juga dapat menggunakan Faktoriasi Prima dengan memanfaatkan pohon faktor untuk mempermudah kita mencari Faktor dari bilangan yang akan kit acari nilai FPBnya.

Ø  Contoh kita akan cari FPB dari 24 dan 32.

Kita dapat menuliskan hasil poho faktor tersebut kedalam faktorisasi prima

24 = 2 x 2 x 2 x 3 atau 2³ x 3

32 = 2 x 2 x 2 x 2 x 2 atau  2⁵

Setelah itu kita ambil faktor yang sama dan dengan pangkat terkecil yaitu 2³ . maka FPB dari 24 dan 32 yaitu 2³ atau 8.

Muat

Pengertian Faktorisasi Prima Dan Contohnya

 

        1.     Pengertian

Salah satu cara untuk menguraikan bilangan kedalam bentuk perkalian adalah dengan cara Faktorisasi Prima. Secara definisi Faktorisasi Prima yaitu proses penulisan suatu bilangan sebagai perkalian dari faktor-faktor primanya. Dengan proses Faktorisasi Prima, suatu bilangan dapat ditulis sebagai perkalian dari faktor-faktor primanya. Metode faktorisasi prima ini bisa sangat berguna untuk mencari nilai KPK dan FPB.

        2.     Contoh Soal

Sebagai contoh kita akan mencari faktorisasi dari 64 dengan menggunakan pohon paktor sebagai salah satu cara untuk mencari faktorisasi dari 64.

   Ø  Faktorisasi Prima dari 64 adalah 

Dalam langkah awal untuk menggunakan cara faktorisasi prima yaitu kita harus membagi angka yang akan dicari dengan bilangan prima terkecil untuk membaginya. Dalam contoh diatas bilangan prima terkecil yang dapat membagi 64 adalah 2. Setelah dibagi sampai mengjhasilkan bilangan prima maka faktorisasi prima sudah selsai. Dari pohon faktor diatas didapat hasil bahwa faktorisasi dari 64 yaitu 64 = 2 x 2 x 2 x 2 x 2 x 2 atau bisa juga ditulis 2⁶.    

   Ø  Faktorisasi Prima dari 25 adalah

       Langkah awal untuk mencari faktorisasi prima dari 25 yaitu menggunakan poho faktor

. 

Setelah didapat pembagian bilangan prima maka proses faktorisasi telah selsai. Jadi untuk faktorisasi dari 25 yaitu 5 x 5 atau bisa di tulis juga 5².

Muat

Pembahasan mengenai Faktor dan Faktor persekutuan

Dalam artikel kali ini kita akan membahas sedikit mengenai faktor dari suatu bilangan dan contoh pembahasan soal. Materi faktor suatu bilangan ini sangatlah penting untuk di kuasai dan lebih lanjut lagi akan bisa mempermudah kita dalam mengerjakan FPB dan KPK.

1. Pengertian Faktor suatu bilangan.

Faktor suatu bilangan yaitu bilangan bulat yang dapat membagi habis suatu bilangan.  Disini membagi habis yaitu Ketika kita membagi suatu bilangan tidak terdapat sisa atau angka dibelakang koma. Sebagai contoh dari bilangan bulat positif yang membagi habis yaitu kita ambil angka 20 maka bilangan yang bisa membagi habis 20 yaitu 1,2,4,5,10,20. Bilangan tersbut bisa kita sebut sebagai faktor dari 20. 

2. Cara menentukan Faktor dari suatu bilangan.

Dalam menentuka faktro dari suatu bilangan terdapat banyak cara untuk mencarinya mulai dari mengkalikan secara mengurut dari angka terkecil sampai menebak angka yang mungkin bisa membagi habis suatu bilangan. Tetapi kunci dari menentukan faktor dari suatu bilangan yaitu kita harus benar paham mengenai perkaian agar lebih mudah untuk menentukan bilangan-bilangan yang merupakan faktor yang di cari.

3. Contoh soal dan pembahasan.

1) Carilah faktor dari 12 . . .

Untuk mencari faktor dari 12 kita harus mengetahui terlebih dahulu perkalian yang menghasilkan 12, Yaitu:

Terlihat bahwa 1,2,3,4,6 jika dikalikan bisa menghasilkan 12 berarti 1,2,3,4,6,12 juga bisa membagi habis 12. Jadi faktor dari 12 yaitu 1,2,3,4,6,12.

2) Carilah faktor dari 25 . . .

Untuk mencari faktor dari 25 kita harus mengetahui terlebih dahulu perkalian yang menghasilkan 25, Yaitu: 

Terlihat bahwa 1,5,25 jika dikalikan bisa menghasilkan 25 berarti 1,5,25 juga bisa membagi habis 25. Jadi faktor dari 25 yaitu 1,5,25

3) Carilah faktor dari 23 . . .

Sebelum kita mencari faktor dari 23 kita haruslah tahu bahwa 23 merupakan bilangan prima yaitu bilangan yang hanya akan habis dibagi oleh satu dan bilangan itu sendiri. Jadi faktor dari 23 yaitu 1 dan 23.

4. Faktor persekutuan

Faktor persekutuan merupakan faktor-faktor yang sama dari dua bilangan atau lebih. Sebagai contoh yaitu faktor persekutuan dari 12 dan 24. Pertama kita harus mengetahui faktor dari masing-masing.

   

Faktor 12 : 1,2,3,4,12

Faktor 24 : 1,2,3,4,6,8,12,24

Setelah mendapat faktor dari masing-masing kemudian kit acari angka yang sama. Didapat angka yang sama yaitu 1,2,3,4,12 jadi jawaban untuk faktor persekutuan dari 12 dan 24 adalah 1,2,3,4,12.

Muat

Mengenal Bilangan Prima beserta contoh soal

1.     Pengertian

Bilangan prima merupakan salah satu bilangan yang terdapat di dalam Matematika. Bilangan prima ini berbeda dengan bilangan yang lain dan mempunyai ciri-ciri yang dapat membedakan antara bilangan prima dengan bilangan yang lain. Untuk menentukan suatu bilangan itu merupakan prima atau tidak yaitu bilangan prima lebih besar dari 1(satu) dan hanya bisa habis dibagi oleh bilangan itu sendiri. Untuk angka satu sudah memenuhi salah satu syarat sebagai bilangan prima tetapi angka 1 lebih kecil dari 2. Jadi 1 bukan termasuk bilangan prima. Sebagai contoh bilangan prima yaitu 2, 3, 5, 7, 11, 13, 17, 19 ,23 dan seterusnya sampai tak hingga.

 2.   Syarat Bilagan Prima

Syarat yang harus dipenuhi agar suatu bilangan itu di sebut bilangan prima

1.     Lebih besar dari angka 1 (satu) / x > 1

2.     Hanya habis dibagi oleh bilangan 1 dan bilangan itu sendiri.

 3.     Contoh Soal

                1.       Apakah angka 2 merupakan bilangan prima?

Kita teliti lebih dalam mengenai angka 2 apakah benar angka 2 merupakan bilangan prima.

Syarat 1

Lebih besar dari angka 1 (satu) / x > 1 . dan kita tahu bahwa angka 2 itu lebih besar dari satu. Jadi untuk syarat 1 memenuhi.

Syarat 2

Hanya habis dibagi oleh bilangan itu sendiri. Angka dua hanya akan habis dibagi oleh 1 dan 2 (bilangan itu sendiri)

2.     Apakah 11 merupakan bilangan prima?

Syarat 1

Angka 11 lebih besar dari angka 1 jadi syarat satu terpenuhi.

Syarat 2

Angka 11 hanya akan habis dibagi oleh satu atau bilangan itu sendiri (sebelas). Jika 11 dibagi oleh bilangan yang lain semisal 5 hasilnya yaitu berupa koma dan itu tidak habis dibagi. Jadi syarat 2 untuk bilangan 11 terpenuhi dan 11 merupakan bilangan prima.

 

3.     Sebutkan bilangan prima dari 0 sampai 100.

Untuk bilangan prima dari 0 sampai 100 yaitu 

 

 

 

 

 

 

Muat

Konsep Limit Aljabar

 

Pada artikel kali ini kita akan sama-sama membahas mengenai limit fungsi aljabar mulai dari konsep dasar, rumus dan contoh soal. 

 Limit fungsi aljabar mempunyai notasi

 

Pada notasi atau rumus di atas mempunyai arti yaitu jika x mendekati a maka f(x) mendekati nilai L tetapi x≠ a. dan suatu fungsi dikatakan mempunyai nilai limit jika didekati dari kiri dan kanan mempunyai nilai yang sama. 

Jadi ketika nilai limit kiri dan kanan mempunyai nilai yang sama maka fungsi tersebut memiliki nilai limit. Sebagai contoh

 

Pada fungsi diatas untuk semua nilai x anggota bilangan real akan terdefinisi terkecuali  x = 1 .mengapa ini bisa terjadi? kita akan coba memasukan nilai x = 1 kedalam fungsi tersebut.

 

Setelah nilai x = 1 di subsitusikan kedalam fungsi di atas maka menghasilkan nilai 0/0 atau bentuk tak tertentu. Maka terbukti bahwa fungsi tersebut tidak terdefinisi untuk x = 1. Meskipun tidak terdefinisi untuk x = 1 tetapi kita bisa melakukan pendekatan menggunakan konsep limit. Kita akan menggunakan pendekatan menggunakan limit kiri dan kanan.

Pada table tersebut terlihat bahwa jika kita memasukan x mendekati nilai 1 maka nilai f(x) juka cenderung mendekati nilai 2 baik itu didekati dari kiri atau kanan.

                                                                                           

Karena nilai limit kanan dan limit kiri sama dengan 2 maka fungsi di atas memiliki nilai limit, hasil limit fungsi diatas yaitu

 

Selain dengan menggunakan cara table seperti di atas, ada cara lain untuk dapat mempermudah kita dalam mencari nilai limit suatu fungsi. Tetapi sebelum kita mempelajari cara atau metode untuk mencari nilai suatu limit, kita harus paham mengenai sifat-sifat limit fungsi aljabar 

 

Dengan n adalah bilangan bulat positif, k konstanta, f dan g merupakan suatu fungsi yang mempunyai limit di c . 

Setelah mengetahui beberapa sifat-sifat pada limit fungsi aljabar, kita masuk ke cara atau metode untuk mencari nilai limit suatu fungsi. Ada beberapa metode dalam mencari nilai limit, yaitu

• Metode Subsitusi
• Metode Pemfaktoran
• Metode Perkalian Sekawan

1.   Metode Subsitusi

Pada metode subsitusi kita hanya perlu memasukan nilai kedalam variabel kemudian kita hitung hasilnya. Sebagai contoh 

Disini kita hanya perlu memasukan nilai yang mendekati kedalam variabel (x) dan akan langsung mendapat nilai limitnya.

2.   Metode Pemfaktoran

Metode ini digunakan ketika kita menggunakan metode subsitusi tetapi menghasilkan nilai tak terdefinisi. Contoh

 

Pada fungsi diatas untuk semua nilai x anggota bilangan real akan terdefinisi terkecuali  x = 2 . apa jadinya jika kita coba masukan nilai x = 2?  kita akan coba memasukan nilai x = 1 kedalam fungsi tersebut.

 

 

3.     Metode Perkalian Sekawan

Metode yang selanjutnya yaitu perkalian sekawan. Metode ini digunakan ketika kita menemukan fungsi yang berbentuk akar. Selain dapat mempermudah kita untuk mencari nilai limit, metode ini juga untuk menghindari kita dari nilai irasional dan memudahkan untuk mensubsitusikannya langsung. Sebagai contoh

 

Maka dari itu kita menggunakan strategi yaitu metode perkalian sekawan.

 

Muat