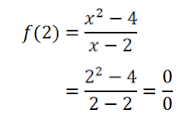Pada artikel kali ini kita akan sama-sama membahas mengenai limit fungsi aljabar mulai dari konsep dasar, rumus dan contoh soal.
Limit fungsi aljabar mempunyai notasi
Pada notasi atau rumus di atas mempunyai arti yaitu jika x mendekati a maka f(x) mendekati nilai L tetapi x≠ a. dan suatu fungsi dikatakan mempunyai nilai limit jika didekati dari kiri dan kanan mempunyai nilai yang sama.
Jadi ketika nilai limit kiri dan kanan mempunyai nilai yang sama maka fungsi tersebut memiliki nilai limit. Sebagai contoh
Pada fungsi diatas untuk semua nilai x anggota bilangan real akan terdefinisi terkecuali x = 1 .mengapa ini bisa terjadi? kita akan coba memasukan nilai x = 1 kedalam fungsi tersebut.
Setelah nilai x = 1 di subsitusikan kedalam fungsi di atas maka menghasilkan nilai 0/0 atau bentuk tak tertentu. Maka terbukti bahwa fungsi tersebut tidak terdefinisi untuk x = 1. Meskipun tidak terdefinisi untuk x = 1 tetapi kita bisa melakukan pendekatan menggunakan konsep limit. Kita akan menggunakan pendekatan menggunakan limit kiri dan kanan.
Pada table tersebut terlihat bahwa jika kita memasukan x mendekati nilai 1 maka nilai f(x) juka cenderung mendekati nilai 2 baik itu didekati dari kiri atau kanan.
Karena nilai limit kanan dan limit kiri sama dengan 2 maka fungsi di atas memiliki nilai limit, hasil limit fungsi diatas yaitu
Selain dengan menggunakan cara table seperti di atas, ada cara lain untuk dapat mempermudah kita dalam mencari nilai limit suatu fungsi. Tetapi sebelum kita mempelajari cara atau metode untuk mencari nilai suatu limit, kita harus paham mengenai sifat-sifat limit fungsi aljabar
Dengan n adalah bilangan bulat positif, k konstanta, f dan g merupakan suatu fungsi yang mempunyai limit di c .
Setelah mengetahui beberapa sifat-sifat pada limit fungsi aljabar, kita masuk ke cara atau metode untuk mencari nilai limit suatu fungsi. Ada beberapa metode dalam mencari nilai limit, yaitu
- Metode Subsitusi
- Metode Pemfaktoran
- Metode Perkalian Sekawan
Pada metode subsitusi kita hanya perlu memasukan nilai kedalam variabel kemudian kita hitung hasilnya. Sebagai contoh
Disini kita hanya perlu memasukan nilai yang mendekati kedalam variabel (x) dan akan langsung mendapat nilai limitnya.
2. Metode Pemfaktoran
Metode ini digunakan ketika kita menggunakan metode subsitusi tetapi menghasilkan nilai tak terdefinisi. Contoh
Pada fungsi diatas untuk semua nilai x anggota bilangan real akan terdefinisi terkecuali x = 2 . apa jadinya jika kita coba masukan nilai x = 2? kita akan coba memasukan nilai x = 1 kedalam fungsi tersebut.
3. Metode Perkalian Sekawan
Metode yang selanjutnya yaitu perkalian sekawan. Metode ini digunakan ketika kita menemukan fungsi yang berbentuk akar. Selain dapat mempermudah kita untuk mencari nilai limit, metode ini juga untuk menghindari kita dari nilai irasional dan memudahkan untuk mensubsitusikannya langsung. Sebagai contoh
Maka dari itu kita menggunakan strategi yaitu metode perkalian sekawan.
Untuk Navigasi Lengkap Silahkan Kunjungi Peta Situs